$132$ 模式的进阶,求 $1324$ 模式 的个数:枚举 4 ,求 4 左边 132 模式的数量
前言
四元上升组定义:一个组 $(i, j, k, l)$ 满足以下条件:
- $0 <= i < j < k < l < n $ 且
- $nums[i] < nums[k] < nums[j] < nums[l] $。
在数组中是这样的:
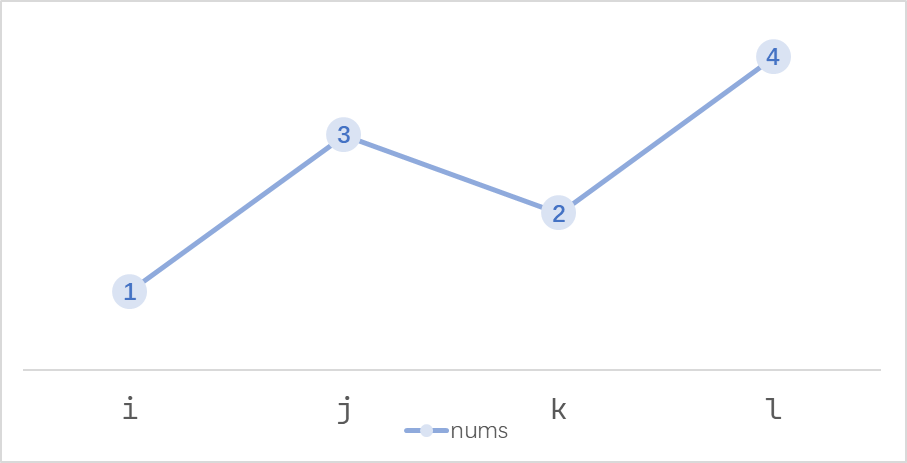
这里称之为 $1324$ 模式,如果有疑惑,请先AC:456. 132 模式
AC后,可以先思考下:返回长度 $n-2$ 的数组,记录每个 $j$ 下有多少个 $132$ 模式。
$ nums[i] < nums[k] < nums[j] \quad \quad i<j<k $
解法的时间复杂度应当不超过 $\mathcal{O}(n^2)$
比如 示例3:$nums = [-1,3,2,0]$
$j=1$ 下有 $2$ 个 $132$ 模式的的子序列:$[-1, 3, 2]$、$[-1, 3, 0]$
$j=2$ 下有 $1$ 个 $132$ 模式的的子序列:$[-1, 2, 0]$
那么答案为:$ans = [2,1]$
注意:
本篇内容是尝试去拆分 佬@DestinyGod 题解最简洁代码,从而得到的个人理解。
思路
题目要求统计数组中有多少个 $1324$ 模式。
题目数据范围:$4 <= nums.length <= 4000$,意味着代码的时间复杂度应为 $\mathcal{O}(n^2)$,部分语言 $\mathcal{O}(n^2 \log n)$ 也可以AC。
枚举 j 和 l
时间复杂度度 $\mathcal{O}(n^2)$ 可以过,可以枚举最大的 $3$ 和 $4$ ,设索引分别为 $j$ 和 $l$。
如果知道在区间 $[0, l]$ 内,以 $j$ 为 $3$ 的 $132$ 模式的数量,记为 $count[l][j]$,并在双重循环中累加起来,那就是答案了。
伪代码:
// 从小到大枚举 l 统计答案
// 如果 nums[j] < nums[l],那么有 `j为3, l为4` 的 `1324模式`
// 答案应当加上以 `j为3` 的 `132模式` 的数量
for l := 0; l < n; l++ {
for j := 0; j < l; j++ {
if nums[j] < nums[l] { // 符合 1324 模式
ans += count[l][j] // count[l][j] 表示 在区间 [0, l] 内,以 `j为3` 的 `132模式` 的数量
}
}
}
可以看出,这部分代码的时间复杂度是 $\mathcal{O}(n^2)$,如果能在时间复杂度 $\mathcal{O}(n^2)$ 以内预处理好 $count[l][j]$,那么就可以完成此题。
预处理 count[l][j]
需要注意在区间 $[0, l]$ 内,以 $j$ 为 $3$ 的 $132$ 模式的所有数量,等于 所有能满足
$ nums[i] < nums[k] < nums[j] \quad \quad \quad i \in [0, j-1],\ k \in [j+1, l-1] $
$(i, k)$ 的对数
计算 $count[l][j]$,可以借助动态规划的思想。
在区间 $[0, l]$ 内,以 $j$ 为 $3$ 的 $132$ 模式的所有数量 等于 在区间 $[0, l-1]$ 内的数量加上以 $j$ 为 $3$,以 $l$ 为 $2$ 的 $132$ 的数量,记为 $x$,即:
$ count[l][j] = count[l-1][j] + x $
而 $x$ 就是 在 $[0,j-1]$ 区间内,小于 $nums[l]$ 的数量,那如何计算 $x$ 呢?暴力枚举:
x := 0
for j := 0; j < l; j++ {
if nums[j] < nums[l] {
x++
}
}
在加上枚举 $l$ 的实现,就得到 预处理 $count[l][j]$的代码:
// count[l][j] 表示 在 [0, l] 这段区间内,以 `j为3` 的 `132模式` 数量
var count = make([][]int, n)
for l := 0; l < n; l++ {
count[l] = make([]int, l+1)
x := 0 // x 记录 [0, j] 这段区间,有多少个数小于 nums[l]
// 动态规划的思想
for j := 0; j < l; j++ {
// 在 [0, l] 区间,以 `j为3` 的 `132模式` 数量等于在 [0, l-1] 区间内的数量 + 以 `j为3`,以 `l为2` 的 `132模式` 的数量
count[l][j] = count[l-1][j]
// 如果 nums[j] > nums[l],说明 nums[l] 可以作为新的 2,新增的数量:在 [0, j] 区间中小于 nums[l] 的个数,
// 也就是以 `j为3, l为2` 的 `132模式` 中,x 就为 1 的数量。
if nums[j] > nums[l] {
count[l][j] += x
} else
// 如果 nums[j] < nums[l],说明不满足 `132模式`。但是小于 nums[l] 的数量 +1
if nums[j] < nums[l] {
x++
}
}
}
代码
组合代码
组合 枚举 $j$ 和 $l$ 和 预处理 $count[l][j]$ 的代码即可解决本题:
func countQuadruplets(nums []int) int64 {
// 1324 模式
// i < j < k < l
// nums[i] < nums[k] < nums[j] < nums[l]
var n, ans = len(nums), 0
// count[l][j] 表示 在 [0, l] 这段区间内,以 `j为3` 的 `132模式` 数量
var count = make([][]int, n)
for l := 0; l < n; l++ {
count[l] = make([]int, l+1)
x := 0 // x 记录 [0, j] 这段区间,有多少个数小于 nums[l]
// 动态规划的思想
for j := 0; j < l; j++ {
// 在 [0, l] 区间,以 `j为3` 的 `132模式` 数量等于在 [0, l-1] 区间内的数量加上以 `j为3`,以 `l为2` 的 `132模式` 的数量
count[l][j] = count[l-1][j]
// 如果 nums[j] > nums[l],说明 nums[l] 可以作为新的 2,新增的数量:在 [0, j] 区间中小于 nums[l] 的个数,
// 也就是以 `j为3, l为2` 的 `132模式` 中,x 就为 1 的数量。
if nums[j] > nums[l] {
count[l][j] += x
} else
// 如果 nums[j] < nums[l],说明不满足 `132模式`。但是小于 nums[l] 的数量 +1
if nums[j] < nums[l] {
x++
}
}
}
// 从小到大枚举 l 统计答案
// 如果 nums[j] < nums[l],那么有 `j为3, l为4` 的 `1324模式`
// 答案应当加上以 `j为3` 的 `132模式` 的数量
for l := 0; l < n; l++ {
for j := 0; j < l; j++ {
if nums[j] < nums[l] { // 符合 1324 模式
ans += count[l][j] // count[l][j] 表示 在区间 [0, l] 内,以 `j为3` 的 `132模式` 的数量
}
}
}
return int64(ans)
}
空间优化
可以发现, 枚举 $j$ 和 $l$ 和 预处理 $count[l][j]$ 的遍历的顺序都是一样的:外层遍历 $l$, 内层遍历 $j$
那么可以一边统计答案,一边预处理$count[l][j]$,同时也可以把 $count[l][j]$ 压缩到一维数组。
- 这就是 题解最简洁代码 的解法
func countQuadruplets(nums []int) int64 {
// 1324 模式
// i < j < k < l
// nums[i] < nums[k] < nums[j] < nums[l]
var n, ans = len(nums), 0
// count[l][j] 表示 在 [0, l] 这段区间内,以 `j为3` 的 `132模式` 数量
// 一边统计答案,一边预处理 count[l][j],并将 count[l][j] 为 一维数组
var count = make([]int, n)
for l := 0; l < n; l++ {
x := 0 // x 记录 [0, j] 这段区间,有多少个数小于 nums[l]
for j := 0; j < l; j++ {
// 动态规划的思想
// 在 [0, l] 区间,以 `j为3` 的 `132模式` 数量等于在 [0, l-1] 区间内的数量 + 以 `j为3`,以 `k为2` 的 `132模式` 的数量
// 如果 nums[j] > nums[l],说明 nums[l] 可以作为新的 2,而新增的数量为:在 [0, j] 区间中小于 nums[l] 的个数,
// 也就是以 `j为3, k为2` 的 `132模式` 中,1 的数量。
if nums[j] > nums[l] {
count[j] += x
} else
// 如果 nums[j] < nums[l],说明有 `j为3, l为4` 的 `1324` 模式
// 并且 在 [0,j] 区间内 小于 nums[l] 的数量 +1
if nums[j] < nums[l] {
ans += count[j]
x++
}
}
}
return int64(ans)
}