LC70. 从爬楼梯上手动态规划

alt text

将简单难度的题目拓展到中等难度

动态规划入门：递归

本题 70. 爬楼梯是非常经典的动态规划入门题，动态规划的核心是找到状态转移方程：当前状态与之前状态的关系。想要找到方程，通常需要我们用自顶向下的方式去思考问题，将一个大问题转化为解决子问题，实现的手段通常为递归。

读题：

每次可以爬 $1$ 或 $2$ 阶；
一共要爬 $n$ 阶；
问爬到 $n$ 阶有多少种方法？

假设当前处于第 $n$ 阶，问：上一步处于哪个阶梯？

答：处于 $n-1$ 或 $n-2$ 阶。因为每次只能爬 $1$ 阶或 $2$ 阶，那么上一步选择爬 $1$ 阶，就会处于 $n-1$ 阶，选择爬 $2$ 阶，就会处于 $n-2$ 阶。

解题思路：

记 $f(n)$ 为爬到 $n$ 阶的方法数，如果知道了 $f(n-1)$ 和 $f(n-2)$ ，两者相加就能得到 $f(n)$ ，即 $f(n) = f(n-1) + f(n-2)$ 。

那又如何求 $f(n-1)$ 和 $f(n-2)$ 呢？令 $n = n-1$ ，就有 $f(n-1) = f(n-2) + f(n-3)$ ，可以发现，解决的手段就是递归。

用到了递归，就需要确定递归边界。式子中最小为 $n-2$ ，那么有 $n-2 >= 0$ ，所以 $n_{min}=2$ ，即最后一次递归为 $f(2) = f(1) + f(0)$ 。示例一还很贴心的解释了如何确定初始值 $f(2) = 1 + 1 = 2$ ，因此 $f(0) = 1; f(1) = 1$ 。

如果你足够熟悉，会发现这个公式就是斐波那契数的通项公式： 509. 斐波那契数。不同点仅有：爬楼梯的初始值是 $f(0) = 1; f(1) = 1$ ; 斐波那契数的是 $f(0) = 0; f(1) = 1$ 。

因此只需要修改下初始值就能解答此题：

func climbstairs(n int) int {
	var fib func (n int) int
	fib = func (n int) int {
		if n == 0 || n == 1{
			return 1
		}
		return fib(n - 2) + fib(n - 1)
	}
	return fib(n)
}

不过对于题目的数据范围： $1<=n<=45$ ，不做优化是会超时的，因为

时间复杂度： $O(2^n)$ ，每次递归都需要再计算 $n-1$ 次
空间复杂度： $O(n)$

递归优化：使用缓存

指数级别的时间复杂度，显然是不能满足题目要求的，那么该如何优化呢？

举个例子，先画出 $f(5)$ 的递归的过程，这是一颗二叉树，便于观察它的规律：

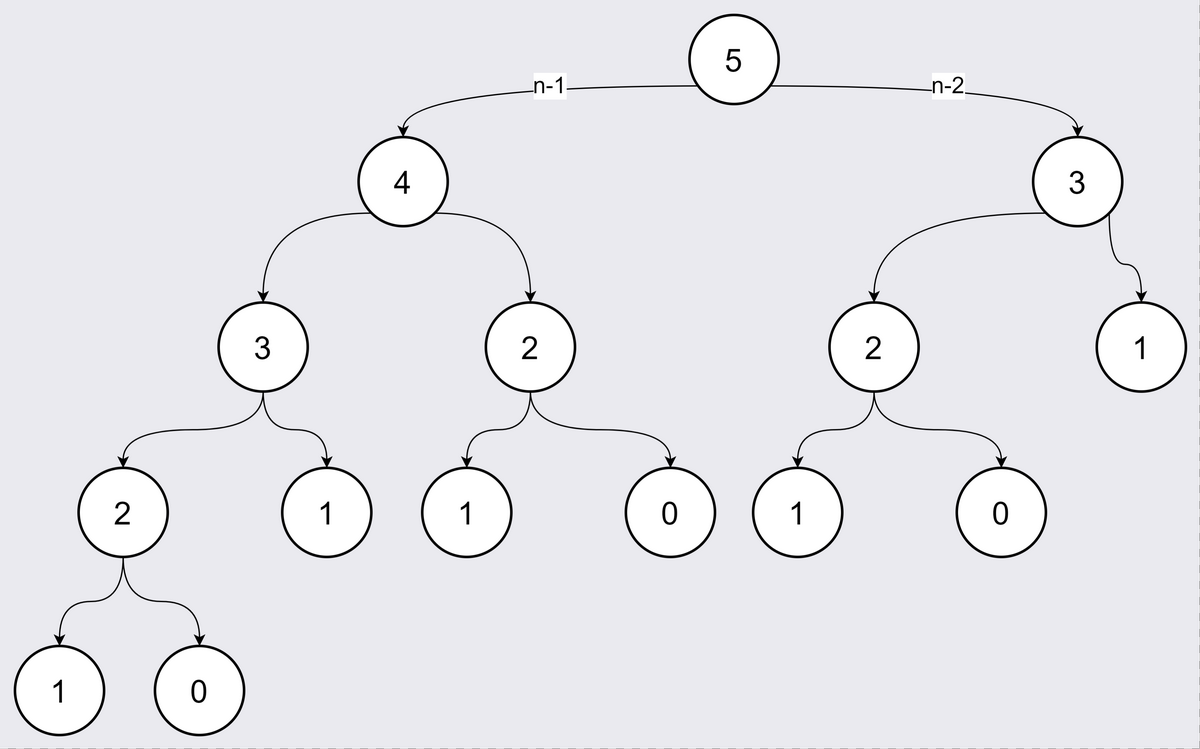
查看这颗二叉树，可以看到 $f(5) = f(4) + f(3)$ ， $f(4) = f(3) + f(2)$ ，这两个地方都会去计算 $f(3)$ ，而这两次计算的结果都是一样的，那么可以在第一次计算的时候，把计算结果保存到 $cache$ 数组或哈希表中。下次计算时，可以直接返回 $cache$ 的结果。优化后的搜索树就变成这样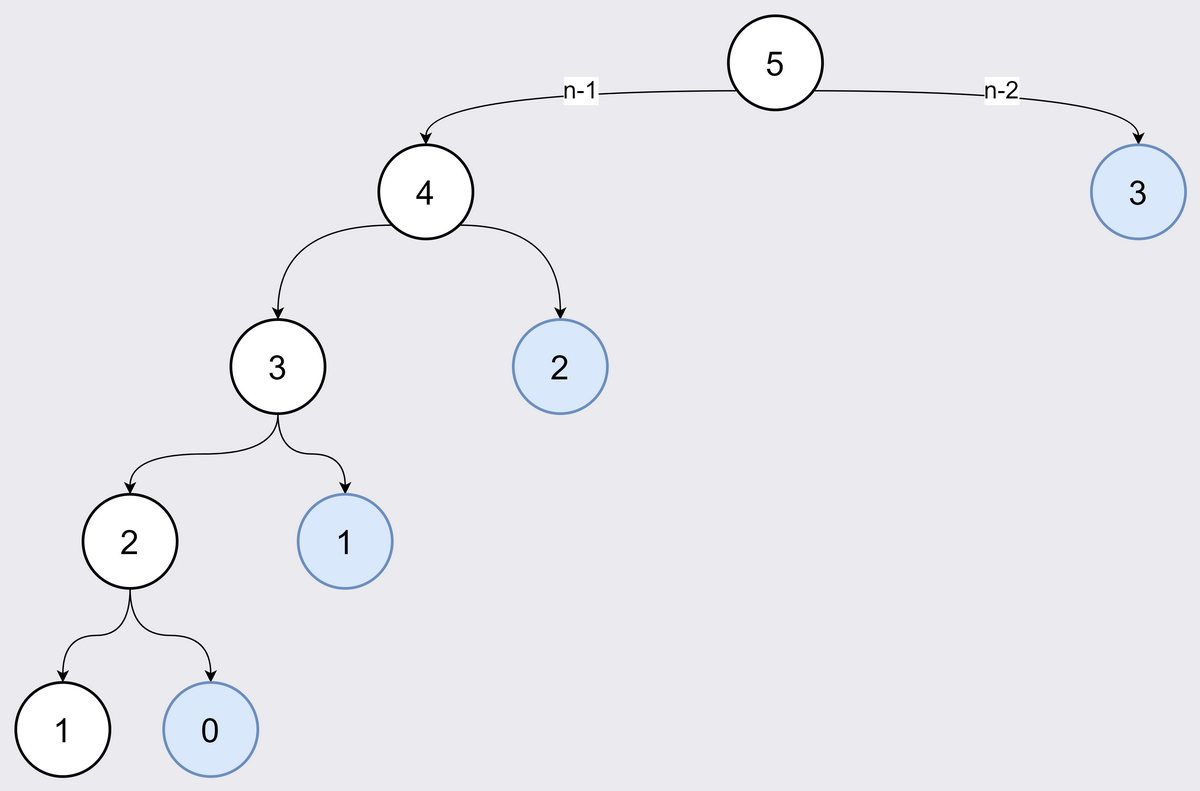：优化后的搜索树只有 $O(n)$ 个节点，因此时间复杂度也优化到了 $O(n)$ 。

代码实现：

func climbStairs(n int) int {
	var cache = make([]int, n+1)
	var fib func (n int) int
	fib = func (n int) int {
		if n == 0 || n == 1{
			return 1
		}
		if cache[n] > 0{
			return cache[n]
		}
		
		res := fib(n - 2) + fib(n - 1)
		cache[n] = res
		return res
	}
	return fib(n)
}

将特例化的题目一般化

对于这道经典题目，如果只是止步于此，那就太可惜了。完全可以稍微修改题目，用于如何归纳出递推公式。

比如，原版是：

每次你可以爬 $1$ 或 $2$ 个台阶

那如果修改成：

每次你可以爬 $k1$ 或 $k2$ 个台阶

就得到了：

爬楼梯2 假设你正在爬楼梯。需要 $n$ 阶你才能到达楼顶。
给你两个正整数 $k1$ 和 $k2$ ，每次你可以爬 $k1$ 或 $k2$ 个台阶。你有多少种不同的方法可以爬到楼顶呢？
```
func climbStairs2(n int, k1 int, k2 int) int
```

又或者再增加可以爬 $3$ 阶的选择，这样就得到了：

爬楼梯3
假设你正在爬楼梯。需要 $n$ 阶你才能到达楼顶。
每次你可以爬 $1$ 或 $2$ 或 $3$ 个台阶。你有多少种不同的方法可以爬到楼顶呢？
```
func climbStairs3(n int) int
```

还可以把爬楼梯2和爬楼梯3的修改组合起来，这样就得到了：

爬楼梯4
假设你正在爬楼梯。需要 $n$ 阶你才能到达楼顶。
给你一个正整数数组 $nums$ ，每次你可以爬 $nums[i]$ 个台阶。你有多少种不同的方法可以爬到楼顶呢？
```
func climbStairs4(n int, nums []int) int
```

完成了 climbStairs4 后，很容易发现：

climbStairs2 是 climbStairs4 在 $len(nums) = 2$ 条件下的特例；
climbStairs3 是 climbStairs4 在 $nums = [1,2,3]$ 条件下的特例。

至此，我们就把一道简单难度的题目拓展为一道中等难度的题目了。另外，这也可以称得上多题一解。